1 Introduction
Xenograft studies involve the transplantation of cells, tissues, or organs from one species, known as the donor species, into another species, called the recipient or host species. In these studies, researchers typically implant human cells, tissues, or tumors into animal models, commonly rodents, to investigate various aspects of human biology, disease progression, and therapeutic interventions. In the context of cancer research, pre-clinical experiments through patient-derived xenografts (PDXs) provide an important scientific tool for the evaluation of novel therapeutic strategies. In particular, PDX studies take into account the high level of response variability between subjects through subject-specific derived replication across treatment groups.
One of the experimental strengths of pre-clinical PDX studies stems from the investigator’s ability to observe the results of a quasi-counterfactual treatment assignment protocol, which sees the same patient-derived tumor potentially treated under different conditions through replication across genetically homogeneous animal models. Eckel-Passow et al. [6] discussed a taxonomy of PDX designs encompassing nested, crossed, and mixed crossed/nested designs, as depicted in Figure 2 of their paper. The nested design involves a naïve hierarchy in which different PDX lines are randomized between treatment groups, before PDX-specific replication is obtained within group and PDX line. While seemingly reasonable, this design does not fully address the possibility of tumor-specific replicates assigned to different treatment groups, and remains susceptible to high levels of tumor-specific response heterogeneity. At the opposite end, a crossed design avoids confounding of randomization and PDX lines by assessing how each level of a factor impacts the outcome with all other factors, i.e. testing all treatments on the same animal grown within each of the PDX lines. As a theoretical construct, this design creates multiple PDX lines and administers multiple drugs within the same animal concurrently, but it often fails to yield meaningful results and lacks feasibility, thus becoming impractical in most experimental settings. Alternatively, incorporating elements from both protocols, a mixed crossed/nested design allows every PDX line to be evaluated for all treatments (crossed design), while allowing subsampling of PDX using animals that cannot be reused across treatment groups (nested design). Effectively addressing potential confounding between PDX line and treatment group, the mixed crossed/nested design has become a common workhorse in PDX research. Using retrospective data from IDH-wildtype glioblastoma preclinical experiments evaluating three treatments across 27 PDX lines, Eckel-Passow et al. [6] demonstrated through empirical simulations that experimental designs employing few animals across many PDX lines can yield robust results and accommodate inter-tumor variability.
The purpose of this paper is to introduce a new statistical R package, named PDXpower, designed for power analysis and determination of the required number of PDX lines and animals per line per treatment group in a PDX experiment structured under the mixed crossed/nested design framework. Notably, statistical power and sample size considerations for testing a treatment effect depend on various factors, including experiment design, statistical model, effect size, and prior information derived from either preliminary data or previous studies. As detailed in Section 2, for uncensored survival time, we employ the mixed effects ANOVA model [16] using PDX as a random effect, which accounts for both intra- and inter-PDX variability, naturally applicable to the mixed crossed/nested design. While several statistical power analysis methods and software packages exist for mixed effects ANOVA models across different analytical platforms, including R [14, 8, 7, 4, 12, 8, 11, 10, 9], SAS [17], and PASS [13], determining the required number of PDX lines and animals per line per treatment group concurrently often necessitates additional coding effort, potentially complex or time-consuming for those less familiar with coding. Our developed R package, PDXpower, addresses this gap, automating the process of determining both parameters simultaneously for the mixed effects ANOVA model. In additional to power analysis based on the mixed effects ANOVA model for uncensored data, our package also includes a module for power calculation with right-censored time-to-event data using Cox’s frailty model [5, 15]. Particularly, this module is tailored for Type 1 censoring of a survival outcome with a fixed administrative censoring time for all animals, which is typical for pre-clinical animal studies. Similar to the mixed effects ANOVA model, the existing power analysis tools for Cox’s frailty models are currently limited to determining the required number of PDX lines with a pre-specified number of animals per line per treatment group [2, 3]. To the best of our knowledge, our R package is the first accessible statistical tool to simultaneously determine both the required number of PDX lines and the number of animals per line per treatment group.
The rest of the paper is organized as follows. In Section 2, we specify the mixed effects ANOVA model for testing treatment effects with uncensored data, and Cox’s frailty model for right-censored data. We also evaluate the Type 1 error rate and rejection power of the statistical test across varying number of PDX lines and animals per line per treatment group though simulations. In Section 3, we provide a tutorial on utilizing our developed package PDXpower to conduct power analysis for different scenarios, with or without preliminary data. Additional remarks are provided in Section 4.
2 Sample Size Determination
2.1 Notation and Statistical Formalization of the Mixed Crossed/Nested Design
For ease of exposition and without loss of generality, we consider comparing outcomes between the control and treatment group, i.e., group A and group B. In the mixed crossed/nested design, for each of n PDX patients/cell lines, we have $2\times m$ implanted animals: m animals are randomized to treatment A and the other m animals are randomized to treatment B. Let $i\in \{1,2,\dots ,n\}$ represent the index of the PDX lines, $j\in \{1,2,\dots ,2m\}$ denote the index of the animals within each PDX line, and ${D_{ij}}$ be a treatment indicator, where ${D_{ij}}=1$ if animal j within PDX line i is in group B, and 0 otherwise. We denote by ${Y_{ij}}$ the outcome of interest, such as the time to death since the beginning of treatment, for animals j within PDX line i, $i=1,\dots ,n$ and $j=1,\dots ,2m$. The observed data will consist of $\{({Y_{ij}},{D_{ij}}):i=1,\dots ,n;j=1,\dots ,2m\}$.
2.2 Statistical Models for Mixed Crossed/Nested Design
We consider two popular analytical frameworks applicable to the mixed crossed/nested design discussed earlier: a mixed effects ANOVA model for uncensored data and Cox’s frailty model for right-censored data.
-
1. Mixed effects ANOVA model: For $i=1,\dots ,n$; $j=1,\dots ,2m$, where ${\beta _{0}}$ is the intercept, β is the treatment effect, ${\alpha _{i}}{\sim _{iid}}N(0,{\tau ^{2}})$ represents an unobserved PDX-specific random effect, and ${\epsilon _{ij}}{\sim _{iid}}N(0,{\sigma ^{2}})$ is a random residual error specific to animals within all PDX lines.
-
2. Cox’s frailty model: For $i=1,\dots ,n$; $j=1,\dots ,2m$, where ${\lambda _{ij}}(t)$ is the hazard function of mouse j within PDX i, ${\lambda _{0}}(t|\lambda ,\nu )$ is a baseline hazard function, following a 2-parameter Weibull distribution $Weibull(\lambda ,\nu )$, with scale and shape parameters λ and ν, respectively, β represents the treatment effect, and ${\alpha _{i}}{\sim _{iid}}N(0,{\tau ^{2}})$ is an unobserved PDX-specific random effect (frailty). As in Model 1, given ${\alpha _{i}}$, ${Y_{ij}}$ are assumed to be mutually independent.
Intuitively, ${\tau ^{2}}$ quantifies the variance in log survival between animals implanted with xenografts from the same patient. Similarly, ${\sigma ^{2}}$ in (2.1), quantifies the variance in average log-survival between groups animals implanted with xenografts from different patients.
Under each of the above models, a Wald-type test can then be conducted for the null hypothesis ${H_{0}}:\beta =0$ to assess the treatment effects at a pre-specified significance level.
2.3 Simulations
We present some simulations to evaluate and illustrate the performance of the Wald test under the mixed effects ANOVA model for uncensored data and Cox’s frailty model for right-censored data for varying number of PDX lines n and animals per line per treatment group m.
2.3.1 Simulation 1: Mixed Effects ANOVA Model for Uncensored Data
We considered two treatment effect scenarios: (a) $\beta =0$, and (b) $\beta =-0.8$, defined as the anticipated difference in mean log(survival time) between the treatment and control groups. For each treatment effect scenario and combination of PDX lines $n=(3,4,5,6,7,8,9,10)$ and animals per line per treatment group $m=(3,4,5,6,7,8)$, we generated 2000 Monte Carlo samples according to the mixed crossed/nested design described in Section 2.1 and the following mixed effects ANOVA model:
where 0.2 is the variance of ${\alpha _{i}}$, meaning that 29% of variability of $\log {Y_{ij}}$ comes from ${\alpha _{i}}$. The estimated rejection power, defined as the proportion of instances where the null hypothesis ${H_{0}}:\beta =0$ is rejected at $\alpha =5\% $ significance level using the mixed effects ANOVA model (2.1), is summarized in Figure 1 for each treatment effect scenario and combination of PDX lines n and animals per line per treatment group m. We note that in our simulations, the intercept value of 5 implies an arbitrary baseline median survival of approximately 148 time units. Alternative values can be used for ease of interpretation and bare little to no effect on power considerations.
(2.3)
\[\begin{aligned}{}\log {Y_{ij}}& =5+{D_{ij}}\beta +{\alpha _{i}}+{\epsilon _{ij}},\\ {} {\alpha _{i}}& \sim N(0,0.2),\\ {} {\epsilon _{ij}}& \sim N(0,0.5),\end{aligned}\]Figure 1
Estimated rejection power of a level $\alpha =0.05$ Wald test for $\beta =0$ using the mixed effects ANOVA model (2.1) based on 2,000 Monte Carlo samples generated from model (2.3) for various combinations of PDX lines $n=(3,4,5,6,7,8,9,10)$ and animals per line per treatment group $m=(3,4,5,6,7,8)$ under two scenarios: (a) $\beta =0$ (left panel), and (b) $\beta =-0.8$ (right panel).
From Figure 1a (left panel), it is evident that the Monte Carlo estimates of the type I error rates closely align with the nominal level $\alpha =0.05$ across all combinations of n and m. Additionally, Figure 1b (right panel) illustrates that increasing the number of PDX lines or animals per line enhances the statistical power to detect the treatment effect, as expected.
2.3.2 Simulation 2: Cox’s Frailty Model for Censored Data
Similar to Simulation 1, we also considered two treatment effect scenarios: (a) $\beta =0$, and (b) $\beta =0.8$, which is defined analogously as in Section 2.3.1. A value of $\beta =0.8$ corresponds to a HR ≈ 2.23, which is a large effect size often assumed in the design of animal studies. For each treatment effect scenario and combination of PDX lines $n=(3,4,5,6,7,8,9,10)$ and animals per line per treatment group $m=(3,4,5,6,7,8)$, we generated 2000 right-censored Monte Carlo samples according to the mixed crossed/nested design described in Section 2.1 and the following Cox’s frailty model:
where ${Y_{ij}}$ follows an exponential distribution with the baseline hazard rate ${\lambda _{0}}(t|\lambda ,\nu )$ of 0.3 and is subject to right-censoring at a pre-determined time point $C=8$, defined as the study duration (end of follow-up), and the intra-PDX correlation is attributed to ${\alpha _{i}}$ with the variance of 0.2. The pre-determined time point $C=8$ is chosen so that the level of censoring is around 10% (7% under $\beta =0.8$ and 12% under $\beta =0$ in our simulation settings). Typically, an animal study’s duration is chosen long enough to minimize the level of censoring.
(2.4)
\[\begin{aligned}{}{Y_{ij}}& \sim 0.3\exp ({D_{ij}}\beta +{\alpha _{i}}),\\ {} {\alpha _{i}}& \sim N(0,0.2),\end{aligned}\]The estimated rejection power of the Wald-type test for testing $\beta =0$ at a significance level of $\alpha =5\% $ based on Cox’s frailty model (2.2) is depicted in Figure 2 for two treatment effect scenarios and various combinations of n and m. It is observed that the Monte Carlo estimates of the type I error rates closely match the nominal level $\alpha =0.05$ across all combinations of n and m (Figure 2a), and increasing the number of PDX lines or animals per line per treatment group enhances the statistical power to detect the treatment effect (Figure 2b). It is worth noting that the sign of the estimated β in model (2.1) is always the opposite to the counterpart in model (2.2) when fitting both models in an animal study. In some cases, they can be the opposite number of each other when ${\epsilon _{ij}}$ follows an extreme value of distribution and ${\lambda _{0}}(t|\lambda ,\nu )$ follows an exponential distribution.
Additionally, we have conducted intensive simulations on multiple scenarios with varying true treatment effect $\beta =(0.2,0.5)$ for the Weibull event outcome or the log-normal outcome. The results and their implications are provided in the Supplementary Material.
Figure 2
Estimated rejection power of a level $\alpha =0.05$ Wald test for $\beta =0$ using Cox’s frailty model (2.2) based on 2000 Monte Carlo samples generated from model (2.4) for various combinations of PDX lines $n=(3,4,5,6,7,8,9,10)$ and animals per line per treatment group $m=(3,4,5,6,7,8)$ under two scenarios: (a) $\beta =0$ (left panel), and (b) $\beta =0.8$ (right panel).
2.4 Statistical Power Calculation and Sample Size Determination via Simulation
We now outline a simulation-based strategy to obtain Monte Carlo estimate of the statistical power for assessing a treatment effect using the mixed crossed/nested design in PDX animal experiments. This strategy is based on the mixed effects ANOVA model (2.1) for uncensored data and Cox’s frailty model (2.2) for right-censored data, as discussed in Sections 2.4.1 and 2.4.2, respectively.
2.4.1 Simulation-based Power Calculation for the Mixed Crossed/Nested Design with Uncensored Data
To perform simulation-based power calculation for the mixed crossed/nested design with uncensored data using the mixed effects ANOVA model, the following information must be determined a priori:
-
i. The hypotheses: ${H_{0}}:\beta =0$ vs ${H_{a}}:\beta ={\beta _{1}}$, where ${\beta _{1}}$ = anticipated difference in mean log(survival time) between the treatment and control groups.
-
ii. Statistical significance level α. It is a commonly used threshold to control the Type 1 error rate, the probability of concluding the results are statistically significant when, in reality, they were arrived at purely by chance.
-
iii. Sample sizes n and m. n is the number of PDX lines and m is the number of animals per PDX line per treat group.
-
iv. Error variance ${\sigma ^{2}}$ in the mixed effects ANOVA model (2.1). This parameter quantifies the unexplained variation across PDX lines and animals.
-
v. Inter-PDX variability ${\tau ^{2}}$. It quantifies the inter-PDX variation across PDX lines.
-
vi. The number of Monte Carlo replicates sim.
With the above priori information, we employ the following simulation strategy for power calculation and subsequently determine the number of PDX lines n and number of animals m per PDX line per group within the mixed effects ANOVA model framework for uncensored data.
-
1. Define a range of feasible values for n and a range of feasible values for m. Subsequently, for every combination of n and m, follow the subsequent steps.
-
3. Fit the mixed effects ANOVA model (2.1) on the simulated data and test ${H_{0}}:\beta =0$ at significance level α.
-
4. Repeat steps 2 and 3 over sim Monte Carlo samples. Calculate the estimated power as the proportion of instances where the null hypothesis ${H_{0}}:\beta =0$ is rejected.
-
5. Given a desired power, say 80%, determine the minimal required number of PDX lines and number of animals per line per treatment group by examining the estimated power across all combinations of n and m.
2.4.2 Simulation-based Power Calculation for the Mixed Crossed/Nested Design with Right-censored Data
To conduct simulation-based power calculation for the mixed crossed/nested design with right-censored data using Cox’s frailty model (2.2), the following priori information are required.
-
i. The hypotheses: ${H_{0}}:\beta =0$ vs ${H_{a}}:\beta ={\beta _{1}}$, where ${e^{{\beta _{1}}}}$ represents the hazard ratio between the treatment and control groups.
-
ii. Statistical significance level α.
-
iii. Sample sizes n and m. n is the number of PDX lines and m is the number of animals per PDX line per treat group.
-
iv. Inter-PDX variability ${\tau ^{2}}$. It is the variance of PDX-specific random effect ${\alpha _{i}}\sim N(0,{\tau ^{2}})$, which quantifies the inter-PDX variation across PDX lines.
-
v. Baseline hazard in Cox’s frailty model (2.2). Most existing power analysis tools for survival data assume the exponential or Weibull distribution as a working model for the baseline hazard, which is also adopted in our simulation-based power calculation.
-
vi. Duration of follow-up. In pre-clinical studies, it is typical to initiate treatment for all animals simultaneously and follow them until the conclusion of the study, resulting in type I censoring of the time-to-event outcome at the end of the follow-up period.
-
vii. The number of Monte Carlo replicates sim.
With the above priori information, the following simulation strategy will be used for power calculation and subsequently determine the number of PDX lines n and number of animals m per PDX line within Cox’s frailty model framework for right-censored data.
-
1. Define a range of feasible values for n and a range of feasible values for m. Subsequently, for every pairing of n and m, follow the subsequent steps.
-
2. Generate a Monte Carlo sample $\{({Y_{ij}},{D_{ij}}),\hspace{2.5pt}i=1,\dots ,n;j=1,\dots ,2m\}$ according to the mixed crossed/nested design described in Section 2.1 and Cox’s frailty model (2.2) with the above priori information i–vii. Then, form a right-censored sample $\{({\tilde{Y}_{ij}},{\delta _{i}},{D_{ij}})\equiv (\min \{{Y_{ij}},C\},I({Y_{ij}}\le C),{D_{ij}}):\hspace{2.5pt}i=1,\dots ,n;j=1,\dots ,2m\}$.
-
3. Fit Cox’s frailty model (2.2) on the simulated data and test ${H_{0}}:\beta =0$ at significance level α.
-
4. Repeat steps 2 and 3 over sim Monte Carlo samples. Calculate the estimated power as the proportion of instances where the null hypothesis ${H_{0}}:\beta =0$ is rejected.
-
5. Given a desired power, say 80%, determine the minimal required number of PDX lines and number of animals per line per treatment group by examining the estimated power across all combinations of n and m.
3 A Hands-On Tutorial of PDXpower
We have created an R package, PDXpower, to implement the simulation-based power analysis strategy outlined in the previous section. This package functions as a user-friendly analytical tool for determining the required number of PDX lines and animals per line per treatment group under the mixed crossed/nested design for preclinical PDX experiments. Below, we offer practical guidelines and illustrative examples, demonstrating the utilization of PDXpower for designing preclinical PDX experiments for both uncensored and censored data.
3.1 Power Analysis for the Mixed Crossed/Nested Design with Uncensored Data
3.1.1 Power Analysis Based on Preliminary Data
In certain pre-clinical studies, researchers may possess preliminary data from initial or related experimental explorations before embarking on a larger study. Priori information, as discussed in Section 2.4.1, can be derived from the preliminary data, aiding simulation-based power analysis to determine the required number of PDX lines and animals per line per treatment group.
First, install and load the package in a local RStudio environment by running the following code:
For illustration purpose, we have generated an uncensored preliminary dataset named animals1 through simulation, which is stored in our package. The animals1 dataset comprises 18 animals and includes three columns: ID (PDX line ID number), Y (survival time of each animal), and Tx (treatment indicator with 1 for treatment and 0 for control). A screenshot of this dataset, generated as an output of the following R code, is displayed below.
Next, a call to the function PowANOVADat first fits the mixed effects ANOVA model (2.1) on animals1. Subsequently, using the resulting parameter estimates as prior information, it conducts simulations to obtain Monte Carlo estimates of the power function across various sample size combinations.
The inputs for the function PowANOVADat include data, formula, the random effect specification random, the number of PDX lines n, the number of animals m, and the number of Monte Carlo replicates sim. Here, we assume that within-PDX correlation is controlled by the within-subject random effect ${\alpha _{i}}$, i.e., random intercept, so we specify random = ∼ 1|ID. The output, saved in PowTab, is shown below.
One can also visualize the results from the above table, as shown in Figure 3, by calling the function plotpower in our package PDXpower.
where ylim specifies the range of the y-axis in the plot.
Figure 3
Power curve of the illustrating example for the mixed effects ANOVA model with preliminary data.
It is observed from Figure 3 that to achieve approximately 80% power at a 5% significance level, the minimal sample size of PDX lines and animals per arm per line per treatment group can be any of the following $(n,m)$ combinations: $\{(3,4),(4,3),(6,2)\}$. An investigator can then decide which combination to choose based on the feasibility of the study. For example, if it is feasible to employ 6 PDX lines, one may prefer to choose the (6, 2) combination to ensure the maximum possible information on PDX line heterogeneity, resulting in a total of 24 animals (6 PDX lines * 2 treatments * 2 animals per line per treatment group).
3.1.2 Power Analysis Without Preliminary Data
When preliminary data on the treatment under investigation are not available, one may conduct power analysis using relevant information from previous or related studies to estimate the necessary priori information, sometimes incorporating additional model assumptions. Table 1 provides a summary of the required information for power calculations using the mixed effects ANOVA model for the mixed crossed/nested PDX experimental design in the absence of preliminary data.
Table 1
Parameter value elicitation for Log-Normal distributed data for given number of PDX lines n and animals per cell line m.
| Parameter | Interpretation | Values |
| ANOVA | ||
| ctl.med.surv | Median survival in the control arm | Any positive number |
| tx.med.surv | Median survival in the treatment arm | Any positive number |
| ${\sigma ^{2}}$ | Error variance | Any positive number (set ${\sigma ^{2}}=1$ as default) |
| icc | Intra-PDX correlation coefficient | 0 < icc < 1 (set icc = 0.1 as default) |
If one assumes the time-to-event outcome follows a log-normal distribution, then a power analysis will be performed using the mixed effects ANOVA model. The underlying model assumptions require specifying a median survival time in the control and treatment groups, an error variance (${\sigma ^{2}}$, set 1 as default) for the log-survival distribution, and the intra-PDX correlation coefficient (icc, set 0.10 as default), quantifying the proportion of PDX heterogeneity over the total variation, i.e., ${\tau ^{2}}/({\tau ^{2}}+{\sigma ^{2}})$. For example, assuming a median survival of 2.4 time units (days, months, etc.) in the control group, 7.2 time units in the treatment group, and an intra-PDX correlation coefficient icc=0.10, a call to the function PowANOVA generates log-normal Monte Carlo samples (see equation (2.3)) and conducts Monte Carlo simulation-based power calculation over sample size combinations, as shown below:
The output, saved in PowTab, is shown below.
One can also visualize the results from the above table, as shown in Figure 4, by calling the function plotpower in our package PDXpower.
Figure 4
Power curve of the illustrating example for the mixed effects ANOVA model when there is no preliminary data available.
Likewise in Section 3.1.1, the above table displays the power for each combination of n and m, calculated as the proportion of rejecting the null hypothesis $\beta =0$ based on Monte Carlo samples generated from a ANOVA mixed effect model (2.3). It is observed from Figure 4 that to achieve approximately 80% power at a 5% significance level, the minimal sample size of PDX lines and animals per arm per line per treatment group can be any of the following $(n,m)$ combinations: $\{(3,5),(5,3),(7,2)\}$.
3.2 Power Analysis for the Mixed Crossed/Nested Design with Censored Data
If some of the animals are alive (right-censored) at the end of an experiment, then Cox’s frailty model (2.2) should be considered to account for the censoring information.
3.2.1 Power Analysis Based on Preliminary Data
Similar to Section 3.1.1, we have generated a censored preliminary dataset named animals2 through a simulation, which is stored in our package. This animals2 dataset comprises 18 animals and includes four columns: ID (PDX line ID number), Y (survival time of each mouse), Tx (treatment indicator with 1 for treatment and 0 for control), and status (death status with 1 for dead and 0 for alive). A screenshot of this dataset, produced as an output of the following R code, is depicted below.
After loading animals2 in Rstudio, a call to the function PowFrailtyDat derives the required priori information by fitting Cox’s frailty model (2.2) on animals2, and subsequently performs simulation-based power analysis for Cox’s frailty model (2.2) using the derived priori information for various sample size combinations.
The inputs for the function PowFrailtyDat include data, formula, the number of PDX lines n, the number of animals m, Ct duration of follow-up, and censor whether type I censoring is considered (Ct is then specified if TRUE), and the number of Monte Carlo replicates sim. The output, saved in PowTab, is shown below.
Similarly, one may generate a graphical representation of the estimated power listed in the above table, as shown in Figure 5, by calling the function plotpower: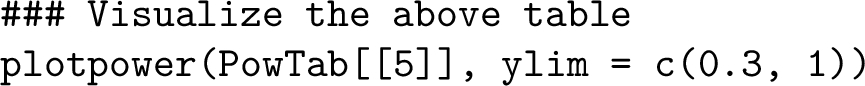 
It is observed from Figure 5 that to achieve approximately 80% power at a 5% significance level, the minimal sample size of PDX lines and animals per arm per line per treatment group can be any of the following $(n,m)$ combinations: $\{(3,8),(4,6),(5,5),(6,4),(7,3)\}$.
3.2.2 Power Analysis Without Preliminary Data
Similar to Section 3.1.2, when preliminary data on the treatment under investigation are not available, Table 2 provides a summary of the required information for power calculations using Cox’s frailty model for the mixed crossed/nested PDX experimental design if one assumes the time-to-event outcome follows a Weibull distribution.
The power calculations in the following example assume a constant hazard ($\nu =1$, set as default), endpoint of the study period (Ct=12), and an approximate variance of the log survival across PDX lines (${\tau ^{2}}=0.1$, set as default, i.e., 0.31 unit of standard deviation in treatment effect β across PDX lines).
Table 2
Parameter value elicitation for Weibull distributed data for given number of PDX lines n and animals per cell line m.
| Parameter | Interpretation | Values |
| Cox’s frailty | ||
| ctl.med.surv | Median survival in the control arm | Any positive number |
| tx.med.surv | Median survival in the treatment arm | Any positive number |
| ν | Baseline Weibull shape parameter | $\nu =1$ constant hazard, default |
| $\nu \gt 1$ increasing hazard | ||
| $\nu \lt 1$ decreasing hazard | ||
| ${\tau ^{2}}$ | Heterogeneity of PDX lines. | ${\tau ^{2}}=0$: no heterogeneity |
| − Set to assumed variance in | ${\tau ^{2}}\gt 0$: heterogeneity | |
| log survival between PDX lines | set ${\tau ^{2}}=0.1$ as default |
The output, saved in PowTab, is shown below.
Similarly, one may generate a graphical representation of the estimated power listed in the above table, as shown in Figure 6, by calling the function plotpower: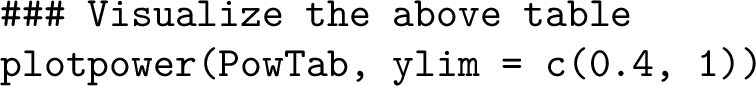 
It is observed from Figure 6 that to achieve approximately 80% power at a 5% significance level, the minimal sample size of PDX lines and animals per arm per line per treatment group can be any of the following $(n,m)$ combinations: $\{(3,5),(4,4),(5,3),(7,2)\}$.
4 Discussion
We have introduced an R package, ‘PDXpower’, designed for simultaneously determining the required number of both PDX lines and animals per line per treatment group for PDX experiments under the mixed crossed/nested design for either uncensored or right-censored time-to-event outcomes. We have also provided step-by-step tutorials for its utilization, accommodating scenarios with or without preliminary data. For a right-censored outcome, our package is tailored to type I censoring because it is typical in a PDX experiment for all animals to start treatment at the same time and subsequently be subject to right-censoring by the same administrative censoring at the end of follow-up.
Our power calculation strategy is simulation-based, involving fitting either the mixed effects ANOVA model for uncensored outcomes or Cox’s frailty model with a normal random effect for right-censored outcomes over a large number of Monte Carlo samples. We have implemented a parallel computing strategy in our package to speed up the computation. Based on our experience, our package is fast for the mixed effects ANOVA model for uncensored outcomes as it took around 0.5 minutes to run 500 Monte Carlo samples to generate Figure 3 on a MacBook Pro with 8-Core M1 Pro and 16GB RAM running MacOS. However, it took about 20 minutes to generate the power curves in Figure 5 based on Cox’s frailty model for right-censored outcomes. One could obtain results more quickly by considering a coarser grid for n and m, resulting in fewer combinations. To enhance the computational efficiency of power calculation for censored data, one could also explore alternate working models, such as different frailty models like the gamma frailty model [2] or standard fixed-effects Cox models treating PDX as fixed effects. Further investigations into these models are warranted.
While the possibility to assign multiple animals to the same PDX line allows for meaningful gains in power, in the evaluation of competing designs, it is important to account for clinical generalizability. Therefore, for a given effect size and power, designs maximizing the number of independent PDX lines are often preferred to designs maximizing the number of animals per PDX line.
In choosing whether to use a Cox’s frailty model vs. a mixed-effects model to power a study, the investigator should decide if the study will generate time-to-event data with possible censoring (fixed follow-up within which not all animals may experience the event of interest) or if all survival outcomes are expected to be observed without censoring. In the first case, using a Cox frailty model is more appropriate and power figures may be obtained in relation to different censoring scenarios. In the latter case (no censoring), the use of a mixed effects model may lead to simpler design considerations.
The sample size calculation paradigm introduced in this manuscript can be generalized to include variations in the study design structure as in [6]. Similarly, for studies requiring multiple measurements per animal, a simple extension of our framework would consider including a second level of nested random effects/random frailties at the animal level.
Software
An R package, PDXpower, designed for conducting simulation-based power analysis in this paper, is publicly available at The Comprehensive R Archive Network (https://CRAN.R-project.org/package=PDXpower).
Supplementary Material
We conducted additional simulations across multiple scenarios with varying true treatment effects (β) for the Weibull event outcome and the log-normal outcome. Estimates of rejection power under the alternative hypothesis are presented in Tables S1–S4. The results show that rejection power estimates are generally lower across all sample sizes of PDX lines and animals when the true β is smaller. When the true $\beta =0.2$ and other parameters are consistent with those in the main text, it was observed that none of the chosen combinations of PDX line and animal sample sizes were sufficient to achieve the desired rejection power, such as 80%. However, larger treatment effects are often hypothesized for powering animal experiments, as the observed differences in survival time between the two arms can be noticeably large in many pilot studies.
Table S1
Estimated rejection power of a level $\alpha =0.05$ Wald test for $\beta =0$ using the mixed effects ANOVA model (2.1) based on 2,000 Monte Carlo samples generated from model (2.3) for various combinations of PDX lines $n=(3,4,5,6,7,8,9,10)$ and animals per line per treatment group $m=(3,4,5,6,7,8)$ under $\beta =0.2$.
| $n/m$ | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 0.0995 | 0.0970 | 0.1165 | 0.1275 | 0.1415 | 0.1555 |
| 4 | 0.1045 | 0.1120 | 0.1345 | 0.1580 | 0.1700 | 0.2040 |
| 5 | 0.1165 | 0.1315 | 0.1655 | 0.1965 | 0.2035 | 0.2515 |
| 6 | 0.1325 | 0.1470 | 0.1965 | 0.2195 | 0.2545 | 0.2810 |
| 7 | 0.1415 | 0.1755 | 0.2085 | 0.2375 | 0.2730 | 0.3350 |
| 8 | 0.1590 | 0.1915 | 0.2285 | 0.2670 | 0.2990 | 0.3695 |
| 9 | 0.1815 | 0.2155 | 0.2625 | 0.2920 | 0.3345 | 0.4115 |
| 10 | 0.1930 | 0.2340 | 0.2815 | 0.3215 | 0.3655 | 0.4415 |
Table S2
Estimated rejection power of a level $\alpha =0.05$ Wald test for $\beta =0$ using the mixed effects ANOVA model (2.1) based on 2,000 Monte Carlo samples generated from model (2.3) for various combinations of PDX lines $n=(3,4,5,6,7,8,9,10)$ and animals per line per treatment group $m=(3,4,5,6,7,8)$ under $\beta =0.5$.
| $n/m$ | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 0.3050 | 0.3785 | 0.4810 | 0.5440 | 0.6035 | 0.6750 |
| 4 | 0.3865 | 0.4780 | 0.6015 | 0.6625 | 0.7230 | 0.8130 |
| 5 | 0.4575 | 0.5810 | 0.6920 | 0.7815 | 0.8205 | 0.8920 |
| 6 | 0.5325 | 0.6710 | 0.7735 | 0.8465 | 0.8780 | 0.9390 |
| 7 | 0.6075 | 0.7410 | 0.8285 | 0.8985 | 0.9255 | 0.9685 |
| 8 | 0.6580 | 0.7965 | 0.8745 | 0.9335 | 0.9585 | 0.9850 |
| 9 | 0.7145 | 0.8470 | 0.9075 | 0.9575 | 0.9725 | 0.9915 |
| 10 | 0.7655 | 0.8850 | 0.9320 | 0.9765 | 0.9830 | 0.9960 |
Table S3
Estimated rejection power of a level $\alpha =0.05$ Wald test for $\beta =0$ using Cox’s frailty model (2.2) based on 2000 Monte Carlo samples generated from model (2.4) for various combinations of PDX lines $n=(3,4,5,6,7,8,9,10)$ and animals per line per treatment group $m=(3,4,5,6,7,8)$ under $\beta =0.2$.
| $n/m$ | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 0.0912 | 0.0809 | 0.1040 | 0.0934 | 0.0999 | 0.1106 |
| 4 | 0.0958 | 0.0918 | 0.1130 | 0.1091 | 0.1025 | 0.1295 |
| 5 | 0.0890 | 0.0865 | 0.1162 | 0.1190 | 0.1172 | 0.1444 |
| 6 | 0.0816 | 0.0905 | 0.1125 | 0.1365 | 0.1314 | 0.1602 |
| 7 | 0.0830 | 0.1011 | 0.1267 | 0.1445 | 0.1546 | 0.1824 |
| 8 | 0.0907 | 0.1040 | 0.1341 | 0.1642 | 0.1701 | 0.2007 |
| 9 | 0.0902 | 0.1151 | 0.1541 | 0.1648 | 0.1898 | 0.2114 |
| 10 | 0.1050 | 0.1213 | 0.1657 | 0.1763 | 0.1997 | 0.2307 |
Table S4
Estimated rejection power of a level $\alpha =0.05$ Wald test for $\beta =0$ using Cox’s frailty model (2.2) based on 2000 Monte Carlo samples generated from model (2.4) for various combinations of PDX lines $n=(3,4,5,6,7,8,9,10)$ and animals per line per treatment group $m=(3,4,5,6,7,8)$ under $\beta =0.5$.
| $n/m$ | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 0.1903 | 0.2210 | 0.2785 | 0.3031 | 0.3326 | 0.3909 |
| 4 | 0.2237 | 0.2737 | 0.3482 | 0.3669 | 0.4156 | 0.4843 |
| 5 | 0.2478 | 0.3151 | 0.3996 | 0.4369 | 0.5021 | 0.5724 |
| 6 | 0.2881 | 0.3577 | 0.4451 | 0.5018 | 0.5770 | 0.6393 |
| 7 | 0.3309 | 0.4009 | 0.5096 | 0.5717 | 0.6359 | 0.7106 |
| 8 | 0.3652 | 0.4404 | 0.5688 | 0.6222 | 0.6931 | 0.7644 |
| 9 | 0.4082 | 0.4985 | 0.6099 | 0.6672 | 0.7421 | 0.8067 |
| 10 | 0.4444 | 0.5279 | 0.6680 | 0.7118 | 0.7954 | 0.8445 |
