1 Introduction
Modern experiments can involve a large number of factors. Assuming the effect sparsity principle [3], an experiment with high-dimensional inputs only has a small number of significant factors. Two-level supersaturated designs are often used to identify important factors in screening experiments. Data from such a design can be modeled by a linear model [33] given by
where X is the $n\times p$ design matrix at two levels $-1$ and $+1$, denoted by − and +, $\boldsymbol{y}$ is the response vector of the n observations, $\boldsymbol{\beta }$ is the regression vector of p coefficients, the error vector $\boldsymbol{\epsilon }$ follows the multivariate normal distribution ${N_{n}}(\mathbf{0},{\sigma ^{2}}\mathbf{I})$ and I is the $n\times n$ identity matrix. In X, the first column is the intercept with all +’s and the remaining columns represent the $p-1$ factors. We call X balanced if all its factors consist of an equal number of − and +. If $p=n$, X is a saturated design since all the degrees of freedom are used to estimate $\boldsymbol{\beta }$. If $p\gt n$, X is a supersaturated design since there are not enough degrees of freedom to estimate all components of $\boldsymbol{\beta }$. Construction of supersaturated designs that can accommodate a large number of factors relative to the number of runs has been gaining more and more attention [5, 16, 30, 26]. Popular criteria for comparing supersaturated designs include minimax [2], $E({s^{2}})$ [18, 27] and mean square correlation [8].
It is increasingly common to use modern variable selection methods to analyze data from a supersaturated design and identify important factors [18, 32, 17]. For example, when the number of variables is greater than the number of observations, Osborne, Presnell and Turlach [22] advised to use the Lasso [28] for an initial selection, and then conduct a best subset selection (or similar method) on the variables selected by the Lasso. We focus on discussing and demonstrating our method for the Lasso given its popularity. The proposed designs also work with other penalized regression methods. For variable selection methods such as the Lasso, Zhao and Yu [34] showed that their performance depends more critically on the worst case column correlation than the average column correlation of the design matrix. More details about this point can be found in Appendix B.
Motivated by the importance of controlling the worst case column correlation, we propose a new method to construct supersaturated designs according to the coherence criterion [7], which measures the worst case column correlation. The coherence of an $n\times p$ matrix X is
\[ \mu (\mathbf{X})=\underset{1\le i\lt j\le p}{\max }\frac{|\langle {\boldsymbol{x}_{i}},{\boldsymbol{x}_{j}}\rangle |}{\| {\boldsymbol{x}_{i}}\| \| {\boldsymbol{x}_{j}}\| },\]
where the subscript i denotes the ith column, $\langle \cdot ,\cdot \rangle $ is the dot product and $\| \cdot \| $ is the ${L_{2}}$-norm. Whenever there is no confusion, hereinafter we will drop the symbol X in $\mu (\mathbf{X})$. Clearly, $0\le \mu \le 1$. The smaller μ is, the closer the matrix is to orthogonal. If the columns of X are centered, μ is reduced to the maximum absolute column correlation of X, which is equivalent to the correlation criterion used in [19]. Note that
\[ \mu (\mathbf{X})=\underset{1\le i\lt j\le p}{\max }\frac{|{\boldsymbol{x}_{i}^{\top }}{\boldsymbol{x}_{j}}|}{n}=\frac{{s_{\text{max}}}}{n},\]
where ${s_{\text{max}}}={\max _{1\le i\lt j\le p}}|{\boldsymbol{x}_{i}^{\top }}{\boldsymbol{x}_{j}}|$ is the value used in the minimax criterion [2]. Different from ${s_{\text{max}}}$, $\mu (\mathbf{X})$ reflects the sample size n in its definition. Because the sample size matters in many data analysis procedures, we will construct designs under $\mu (\mathbf{X})$ instead of ${s_{\text{max}}}$ (we will also compare designs with different sample sizes in Section 3.1).Our construction method allows some columns of the design matrix to be unbalanced. Factor balance in a supersaturated design guarantees an accurate estimate of the intercept but unbalance provides other significant benefits in constructing designs. Being unbalanced provides flexibility in controlling the column correlations between every pair of the main effects to achieve a lower average column correlation [29]. Sacrificing the precision of the estimate of the intercept can better estimate the main effects. In addition, allowing unbalance enables us to construct designs with more flexible sizes.
The remainder of the article will unfold as follows. In Section 2, we detail our construction method. In Section 3, we use several examples to demonstrate the advantage of the constructed designs against some benchmark designs for a variable selection problem. We conclude the paper and provide some discussions in Section 4.
2 The Construction Method
2.1 Notation and Definitions
Throughout, “#Balance” denotes the number of balanced columns of a design. Let ${\mathbf{1}_{n}}$ denote the n-dimensional unit vector with $+1$’s. Let I denote the identity matrix. For a matrix A with entries in $\{-1,+1\}$ and an even number of rows, let ${\mathbf{A}^{\ast }}$ denote a matrix obtained by changing the signs of entries in all odd rows and ${\mathbf{A}^{\ast \ast }}$ denote a matrix obtained by changing the signs of entries in all even rows, where ∗ and $\ast \ast $ are two matrix operators. Note that ${(-\mathbf{A})^{\ast \ast }}={\mathbf{A}^{\ast }}$. An $n\times n$ Hadamard matrix H is a matrix with entries in $\{-1,+1\}$ and ${\mathbf{H}^{\top }}\mathbf{H}=n\mathbf{I}$, where n can only be 1, 2 or a multiple of 4.
2.2 Construction Steps
Our construction method expands a $6m\times p$ supersaturated design ${\mathbf{D}_{0}}$ with $\mu \le 1/3$ to a $12m\times 4p$ design with $\mu \le 1/3$, where $m,p$ are positive integers with $6m\lt p$. Partition ${\mathbf{D}_{0}}$ as
where U and L have $4m$ and $2m$ rows, respectively. The proposed method has three steps.
If ${\mathbf{D}_{1}}$ is viewed as a block matrix with four rows, Step 2 applies the operator ∗ to the second row and changes the signs of all entries in the fourth row to obtain ${\mathbf{D}_{2}}$. If ${\mathbf{D}_{2}}$ is viewed as a block matrix with four rows and two columns, Step 3 applies the operator $\ast \ast $ to the first and fourth rows and applies the operator ∗ to the third row to obtain ${\mathbf{D}_{3}}$. It can be proved that the coherence of ${\mathbf{D}_{1}}$, ${\mathbf{D}_{2}}$ and ${\mathbf{D}_{3}}$ is no greater than $1/3$ by Lemmas 1, 2, 3 and Theorem 1 in Appendix A.
Since the design ${\mathbf{D}_{3}}$ from the construction is a $12m\times 4p$ design with $\mu \le 1/3$, repeating the above procedure multiple times with ${\mathbf{D}_{0}}$ being ${\mathbf{D}_{3}}$ produces a class of designs with $({2^{k}}\times 6m)$ rows, $({4^{k}}\times p)$ columns and $\mu \le 1/3$ for every positive integer k.
The only requirement for ${\mathbf{D}_{0}}$ is to be a $6m\times p$ two-level supersaturated design with $\mu \le 1/3$. For a given pair of m and p, different choices of ${\mathbf{D}_{0}}$ yield different forms of ${\mathbf{D}_{3}}$ but all of them have guaranteed small coherence. As suggested by Chen and Lin [6] and Liu, Ruan and Dean [20], a supersaturated design with coherence of $1/3$ can identify most of the important factors.
2.3 Examples
We now provide several examples for the proposed method with different choices of ${\mathbf{D}_{0}}$. In the following examples, we show the first several designs constructed by the proposed method and choose ${\mathbf{D}_{0}}$ to have as many columns as possible.
Example 1.
Let ${\mathbf{D}_{0}}$ be a $6\times 16$ design given by
\[ \left[\begin{array}{r@{\hskip10.0pt}r@{\hskip10.0pt}r@{\hskip10.0pt}r@{\hskip10.0pt}r@{\hskip10.0pt}r@{\hskip10.0pt}r@{\hskip10.0pt}r@{\hskip10.0pt}r@{\hskip10.0pt}r@{\hskip10.0pt}r@{\hskip10.0pt}r@{\hskip10.0pt}r@{\hskip10.0pt}r@{\hskip10.0pt}r@{\hskip10.0pt}r}+& +& +& +& +& +& +& +& +& +& +& +& +& +& +& +\\ {} +& +& +& +& -& -& -& -& -& -& -& -& +& +& +& +\\ {} +& +& -& -& +& +& -& -& +& +& -& -& +& +& -& -\\ {} +& +& -& -& +& +& -& -& -& -& +& +& -& -& +& +\\ {} +& -& +& -& +& -& +& -& +& -& +& -& +& -& +& -\\ {} +& -& +& -& -& +& -& +& +& -& +& -& -& +& -& +\end{array}\right],\]
where − and + denote $-1$ and $+1$, respectively, and its coherence is $1/3$. The coherence of the above design attains the lower bound derived in [31]. The sizes, coherence values and numbers of the balanced columns of the first several designs constructed by the proposed method are given in Table 1.Table 1
Designs Constructed from a $6\times 16$ ${\mathbf{D}_{0}}$.
| Size | μ | #Balance |
| $12\times 64\phantom{xx}$ | 1/3 | 24 |
| $24\times 256\phantom{x}$ | 1/3 | 168 |
| $48\times 1024$ | 1/3 | 840 |
| $96\times 4096$ | 1/3 | 3720 |
| $192\times 16384$ | 1/3 | 15624 |
Example 2.
Let 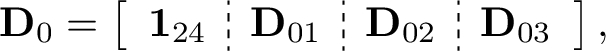
where ${\mathbf{D}_{01}}$ is the $24\times 23$ Plackett and Burman design [23], ${\mathbf{D}_{02}}$ is formed by taking the two-order interaction terms of ${\mathbf{D}_{01}}$ and ${\mathbf{D}_{03}}$ is formed by taking the three-order interaction terms of ${\mathbf{D}_{01}}$. Then ${\mathbf{D}_{0}}$ is a $24\times 2048$ design with $\mu =1/3$. The first 277 columns of this design form the design in [32]. The sizes, coherence values and numbers of the balanced columns of the first several designs constructed by the proposed method are given in Table 2.
Table 2
Designs Constructed from a $24\times 2048$ ${\mathbf{D}_{0}}$.
| Size | μ | #Balance |
| $48\times 8192\phantom{x}$ | 1/3 | 2968 |
| $96\times 32768$ | 1/3 | 18616 |
| $192\times 131072$ | 1/3 | 99064 |
Example 3.
Let ${\mathbf{D}_{0}}$ be the $30\times 59$ design from Lin [18], where an additional column ${\mathbf{1}_{30}}$ is added as the first column. This design has $\mu =0.2$. The sizes, coherence values and numbers of the balanced columns of the first several designs constructed by the proposed method are given in Table 3. This example illustrates that our method can use a design ${\mathbf{D}_{0}}$ with $\mu \lt 1/3$.
Table 3
Designs Constructed from a $30\times 59$ ${\mathbf{D}_{0}}$.
| Size | μ | #Balance |
| $60\times 236\phantom{x}$ | 1/3 | 101 |
| $120\times 944\phantom{xx}$ | 1/3 | 550 |
| $240\times 3776\phantom{x}$ | 1/3 | 2864 |
| $480\times 15104$ | 1/3 | 13156 |
| $960\times 60416$ | 1/3 | 56396 |
Whenever necessary, one can select some columns of the designs constructed for use. Selecting a subset of columns could remain coherence the same or further decrease it, but will never increase coherence. For example, for a given p, first, one can select as many balanced columns as possible. If there are no sufficient balanced columns, then one can select some unbalanced columns to achieve p columns. In addition, one may also select the columns according to an additional criterion such as $E({s^{2}})$.
2.4 Generalization
We now generalize the proposed method to obtain a supersaturated design with μ smaller than $1/3$. Recall that our method partitions ${\mathbf{D}_{0}}$ into two parts. The upper part U has $6mr$ rows and the lower part L has $6m(1-r)$ rows with a partition ratio $r=2/3$. We generalize the original construction by using a different partition ratio and stopping at Step 2. Suppose that ${\mathbf{D}_{0}}$ is an $n\times p$ two-level supersaturated design with $\mu \le t/n$ for $t\in \{2,4,\dots ,n/2\}$ and an even n. Partition ${\mathbf{D}_{0}}$ as in (2.1), where U has $2t$ rows and L has $n-2t$ rows with $r=2t/n$. Define ${\mathbf{D}_{2}}$ as in (2.2). Then ${\mathbf{D}_{2}}$ is the supersaturated design constructed by our generalized method. It can be proved that the coherence of ${\mathbf{D}_{2}}$ constructed here is no greater than $t/n$ by Theorem 2 in Appendix A.
The generalization indicates the possibility of expanding any two-level supersaturated design with $\mu \le 1/2$ and an even number of runs while retaining its coherence. For the original construction, coherence must be no greater than $1/3$ and the initial design must have $6m$ runs but the initial design with p columns can be expanded to a design with $4p$ columns and $\mu \le 1/3$. The generalization only requires that the coherence is no greater than $1/2$ and the initial design has an even number of runs but the initial design with p columns can only be expanded to a design with $2p$ columns and the same coherence. In addition, the number of balanced columns can be fewer than the number of runs for the designs constructed by the generalization. Here is an example.
3 Simulation Study
In this section, we compare the proposed designs with four popular classes of supersaturated designs: Lin’s designs [18], Wu’s designs [32], the Bayesian D-optimal supersaturated designs (Jones, Lin, and Nachtsheim 2008) and the $UE({s^{2}})$-optimal designs [15] for the Lasso problem by simulations. These designs are denoted by “LIN”, “WU”, “BAYES” and “JM” respectively and our proposed designs are denoted by “Proposed”.
Lin’s designs are constructed from the Plackett and Burman design [23]. According to Bulutoglu and Cheng [4], Lin’s designs are $E({s^{2}})$-optimal among all the balanced two-level supersaturated designs. Wu’s designs can be obtained by appending interaction columns to a Hadamard matrix. Bulutoglu and Cheng [4] showed that in certain cases, Wu’s designs are $E({s^{2}})$-optimal among all the balanced two-level supersaturated designs. The Bayesian D-optimal supersaturated design is obtained by the coordinate exchange algorithm [9, 14]. Any n rows of a $p\times p$ Hadamard matrix form a type of $UE({s^{2}})$-optimal design [15, 5].
We simulate data from the linear model in (1.1) with different designs and active coefficients, where the error vector $\boldsymbol{\epsilon }$ follows the standard multivariate normal distribution ${N_{n}}(\mathbf{0},\mathbf{I})$. We use the Lasso to select the active factors and fix the intercept term ${\beta _{1}}$ as active. We repeat the above data generation and variable selection procedure $N=300$ times. We use the “cv.glmnet” function [12] in the R software [24] and calculate $\hat{\boldsymbol{\beta }}$ with “s=lambda.min”.
We conduct simulations using the eight active coefficients settings in Table 5 and denote them as Case 1, $\dots \hspace{0.1667em}$, Case 8, respectively. We use “#Active” to denote the number of active factors. For each group of active coefficients, we consider both the case where they take large values, and the case where they take small values. For example, for ${\beta _{1}}$, ${\beta _{21}}$ and ${\beta _{23}}$, we consider both the case where they take values of 1, 5 and 10, and the case where they take values of 0.1, 1 and 1.5. We let the regression coefficients of all inactive factors be zero and do not write them in Table 5. We neither use a single setting of active coefficients for all the comparisons, nor use all settings in Table 5 for each comparison, because of the following reasons. First, the designs under consideration have different numbers of columns and some designs do not have enough columns for a given setting, which makes the setting not applicable. Second, in practice, the more factors we are considering, the more active factors there tends to be, so we use settings with more active coefficients for designs with large numbers of columns, and settings with fewer active coefficients for designs with small numbers of columns.
Table 5
Active Coefficients Settings.
| Case | #Active | Active Coefficients and Their Values |
| 1 | 2 | ${\beta _{1\phantom{00}}}=1\phantom{.0}\phantom{x}{\beta _{21\phantom{0}}}=5\phantom{.0}\phantom{x}{\beta _{23\phantom{0}}}=10\phantom{.}$ |
| 2 | 2 | ${\beta _{1\phantom{00}}}=0.1\phantom{}\phantom{x}{\beta _{21\phantom{0}}}=1\phantom{.0}\phantom{x}{\beta _{23\phantom{0}}}=1.5\phantom{}$ |
| 3 | 4 | ${\beta _{1\phantom{00}}}=1\phantom{.0}\phantom{x}{\beta _{6\phantom{00}}}=5\phantom{.0}\phantom{x}{\beta _{8\phantom{00}}}=10\phantom{.}\phantom{x}{\beta _{9\phantom{00}}}=10\phantom{.}\phantom{x}{\beta _{26\phantom{0}}}=15\phantom{.}$ |
| 4 | 4 | ${\beta _{1\phantom{00}}}=0.1\phantom{}\phantom{x}{\beta _{6\phantom{00}}}=0.6\phantom{}\phantom{x}{\beta _{8\phantom{00}}}=1.7\phantom{}\phantom{x}{\beta _{9\phantom{00}}}=0.9\phantom{}\phantom{x}{\beta _{26\phantom{0}}}=1\phantom{.0}$ |
| 5 | 4 | ${\beta _{1\phantom{00}}}=1\phantom{.0}\phantom{x}{\beta _{19\phantom{0}}}=5\phantom{.0}\phantom{x}{\beta _{59\phantom{0}}}=14\phantom{.}\phantom{x}{\beta _{143\phantom{}}}=10\phantom{.}\phantom{x}{\beta _{214\phantom{}}}=13\phantom{.}$ |
| 6 | 4 | ${\beta _{1\phantom{00}}}=0.1\phantom{}\phantom{x}{\beta _{19\phantom{0}}}=1.3\phantom{}\phantom{x}{\beta _{59\phantom{0}}}=0.9\phantom{}\phantom{x}{\beta _{143\phantom{}}}=1\phantom{.0}\phantom{x}{\beta _{214\phantom{}}}=1.2\phantom{}$ |
| 7 | 6 | ${\beta _{1\phantom{00}}}=1\phantom{.0}\phantom{x}{\beta _{38\phantom{0}}}=5\phantom{.0}\phantom{x}{\beta _{111\phantom{}}}=5\phantom{.0}\phantom{x}{\beta _{122\phantom{}}}=9\phantom{.0}\phantom{x}{\beta _{123\phantom{}}}=9\phantom{.0}\phantom{x}{\beta _{147\phantom{}}}=9\phantom{.0}\phantom{x}{\beta _{151\phantom{}}}=11\phantom{.}$ |
| 8 | 6 | ${\beta _{1\phantom{00}}}=0.1\phantom{}\phantom{x}{\beta _{38\phantom{0}}}=1.5\phantom{}\phantom{x}{\beta _{111\phantom{}}}=1.5\phantom{}\phantom{x}{\beta _{122\phantom{}}}=1.9\phantom{}\phantom{x}{\beta _{123\phantom{}}}=1.9\phantom{}\phantom{x}{\beta _{147\phantom{}}}=1.9\phantom{}\phantom{x}{\beta _{151\phantom{}}}=2.8\phantom{}$ |
Table 6
Comparison with Lin’s Design.
| Case | #Active | Design | Size | μ | $E({s^{2}})$ | #Balance | AFDR | AMR | MSE | EME |
| 1 | 2 | Proposed | $12\times 27$ | 0.33 | 9.70 | 24 | 0.49 | 0.00 | 0.64 | 7.22 |
| LIN | $14\times 27$ | 0.43 | 7.84 | 26 | 0.59 | 0.00 | 0.93 | 9.18 | ||
| 2 | 2 | Proposed | $12\times 27$ | 0.33 | 9.70 | 24 | 0.51 | 0.02 | 0.74 | 9.15 |
| LIN | $14\times 27$ | 0.43 | 7.84 | 26 | 0.59 | 0.08 | 1.13 | 12.51 | ||
| 3 | 4 | Proposed | $12\times 27$ | 0.33 | 9.70 | 24 | 0.25 | 0.18 | 73.58 | 537.69 |
| LIN | $14\times 27$ | 0.43 | 7.84 | 26 | 0.40 | 0.28 | 230.66 | 794.73 | ||
| 4 | 4 | Proposed | $12\times 27$ | 0.33 | 9.70 | 24 | 0.49 | 0.29 | 2.15 | 18.52 |
| LIN | $14\times 27$ | 0.43 | 7.84 | 26 | 0.64 | 0.53 | 4.19 | 19.79 |
For each design in our simulations, we will show its size, coherence, and number of balanced columns. Although $E({s^{2}})$ is not our focused criterion, we will also show the $E({s^{2}})$ of each design for reference. We use the following four criteria to compare variable selection and model fitting accuracy of each design:
Smaller values of AFDR, AMR, MSE and EME are desirable. Note that AFDR and AMR are computed based on the number of discovered or active coefficients, not the number of discovered or active factors.
-
1. Average False Discovery Rate (AFDR) ${\textstyle\sum _{i=1}^{N}}{\text{FDR}_{i}}\big/N$, where\[ {\text{FDR}_{i}}=\frac{\text{the number of falsely discovered coefficients}}{\text{the number of discovered coefficients}}\]if the discovered model is not a null model, and ${\text{FDR}_{i}}=1$ if the discovered model is a null model.
-
3. Mean Squared Error (MSE) ${\textstyle\sum _{i=1}^{N}}\| \boldsymbol{\beta }-{\hat{\boldsymbol{\beta }}^{(i)}}{\| ^{2}}\big/N$ to estimate $E(\| \boldsymbol{\beta }-\hat{\boldsymbol{\beta }}{\| ^{2}})$.
-
4. Expected Model Error (EME) ${\textstyle\sum _{i=1}^{N}}\| \mathbf{X}\boldsymbol{\beta }-\mathbf{X}{\hat{\boldsymbol{\beta }}^{(i)}}{\| ^{2}}\big/N$ to estimate $E(\| \mathbf{X}\boldsymbol{\beta }-\mathbf{X}\hat{\boldsymbol{\beta }}{\| ^{2}})$.
3.1 Comparison with Lin’s Design
We obtain the $12\times 27$ proposed design by selecting the intercept, the 24 balanced columns and the first two unbalanced columns of the $12\times 64$ design in Example 1. We use Lin’s $14\times 27$ design directly. The result is shown in Table 6, where and in other tables below, the smaller values of the four criteria are in boldface. Table 6 indicates that the proposed design outperforms Lin’s design in terms of variable selection and parameter estimation with the Lasso. In addition, the proposed design has fewer runs than Lin’s design.
To verify that this result is not due to some better property of the selected active factors in one design versus another, we also conducted a follow-up comparison with randomly selected active factors. More specifically, for a given setting in Table 5, we randomly select an #Active number of active factors with the same values given in the setting, and repeat 10 times to get 10 sets of active factors. Then, for each set of randomly selected active factors, we repeat the above data generation and variable selection procedure $N=30$ times for the proposed design and Lin’s design. The final criteria are averaged over the criteria from the 10 sets of active factors, and they can be found in Table 7. According to Table 7, the proposed design still generally outperforms Lin’s design, even with randomly selected active factors. To save computational cost and keep our paper concise, we will omit such a verification for the following comparisons.
Table 7
Comparison with Lin’s Design with Randomly Selected Active Factors.
| Case | #Active | Design | Size | μ | $E({s^{2}})$ | #Balance | AFDR | AMR | MSE | EME |
| 1 | 2 | Proposed | $12\times 27$ | 0.33 | 9.70 | 24 | 0.61 | 0.00 | 5.01 | 9.02 |
| LIN | $14\times 27$ | 0.43 | 7.84 | 26 | 0.61 | 0.00 | 1.59 | 11.58 | ||
| 2 | 2 | Proposed | $12\times 27$ | 0.33 | 9.70 | 24 | 0.58 | 0.09 | 1.34 | 10.83 |
| LIN | $14\times 27$ | 0.43 | 7.84 | 26 | 0.59 | 0.14 | 1.36 | 12.93 | ||
| 3 | 4 | Proposed | $12\times 27$ | 0.33 | 9.70 | 24 | 0.47 | 0.00 | 51.62 | 27.23 |
| LIN | $14\times 27$ | 0.43 | 7.84 | 26 | 0.41 | 0.04 | 33.89 | 135.42 | ||
| 4 | 4 | Proposed | $12\times 27$ | 0.33 | 9.70 | 24 | 0.55 | 0.15 | 2.11 | 13.23 |
| LIN | $14\times 27$ | 0.43 | 7.84 | 26 | 0.45 | 0.27 | 2.13 | 18.56 |
Table 8
Comparison with Wu’s Designs.
| Case | #Active | Design | Size | μ | $E({s^{2}})$ | #Balance | AFDR | AMR | MSE | EME |
| 1 | 2 | Proposed | $12\times 64$ | 0.33 | 9.90 | 24 | 0.65 | 0.00 | 0.95 | 8.41 |
| WU | $12\times 64$ | 0.33 | 11.06 | 63 | 0.54 | 0.00 | 0.89 | 9.03 | ||
| 2 | 2 | Proposed | $12\times 64$ | 0.33 | 9.90 | 24 | 0.66 | 0.05 | 1.20 | 12.46 |
| WU | $12\times 64$ | 0.33 | 11.06 | 63 | 0.56 | 0.04 | 0.98 | 11.22 | ||
| __________________ | _____________________ _ | ________________________ | ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ | ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ | ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ | ________________________ | ___________________ | _________________ | ________________ | _________________ |
| 3 | 4 | Proposed | $24\times 256$ | 0.33 | 21.84 | 168 | 0.41 | 0.00 | 0.96 | 19.96 |
| WU | $24\times 256$ | 0.33 | 23.00 | 255 | 0.65 | 0.00 | 2.08 | 23.25 | ||
| 4 | 4 | Proposed | $24\times 256$ | 0.33 | 21.84 | 168 | 0.67 | 0.04 | 0.94 | 18.20 |
| WU | $24\times 256$ | 0.33 | 23.00 | 255 | 0.68 | 0.14 | 1.76 | 24.90 | ||
| __________________ | _______________________ | __________________________ | __________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ | __________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ | __________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ | __________________________ | _____________________ | ___________________ | __________________ | ___________________ |
| 7 | 6 | Proposed | $48\times 300$ | 0.33 | 93.05 | 299 | 0.62 | 0.00 | 1.76 | 27.15 |
| WU | $48\times 300$ | 0.33 | 41.99 | 299 | 0.75 | 0.00 | 2.52 | 37.94 | ||
| 8 | 6 | Proposed | $48\times 300$ | 0.33 | 93.05 | 299 | 0.71 | 0.00 | 1.74 | 21.65 |
| WU | $48\times 300$ | 0.33 | 41.99 | 299 | 0.77 | 0.01 | 2.58 | 44.09 |
3.2 Comparison with Wu’s Designs
We use the $12\times 64$, $24\times 256$ proposed designs in Example 1 directly. We obtain the $48\times 300$ proposed design by selecting the intercept and the first 299 balanced columns of the $48\times 8192$ design in Example 2. We obtain Wu’s $12\times 64$, $24\times 256$ and $48\times 300$ designs by selecting the first 64 columns of Wu’s $12\times 67$ design, the first 256 columns of Wu’s $24\times 277$ design and the first 300 columns of Wu’s $48\times 1129$ design, respectively. The result shown in Table 8 indicates that the proposed designs are generally better than Wu’s designs in terms of variable selection and parameter estimation with the Lasso. In almost all cases, the proposed designs have better performance while in the first two cases, Wu’s designs perform relatively better.
3.3 Comparison with the Bayesian D-Optimal Supersaturated Designs
We use the $12\times 64$ proposed design in Example 1 directly. We obtain the $24\times 253$ proposed design by selecting the intercept, the 168 balanced columns and the first 84 unbalanced columns of the $24\times 256$ design in Example 1. We first search a $12\times 64$ and a $24\times 256$ Bayesian D-optimal supersaturated design by the JMPő software [13] with 500 random starting designs. We use the $12\times 64$ design directly. We remove the 22th, 134th and 209th columns of the $24\times 256$ design to obtain the $24\times 253$ design used in the simulations since the original searched $24\times 256$ Bayesian D-optimal supersaturated design has $\mu =0.83$. The result shown in Table 9 indicates that the proposed designs generally outperform the Bayesian D-optimal supersaturated designs in terms of variable selection and parameter estimation with the Lasso.
Table 9
Comparison with the Bayesian D-Optimal Supersaturated Designs.
| Case | #Active | Design | Size | μ | $E({s^{2}})$ | #Balance | AFDR | AMR | MSE | EME |
| 1 | 2 | Proposed | $12\times 64$ | 0.33 | 9.90 | 24 | 0.65 | 0.00 | 0.95 | 8.41 |
| BAYES | $12\times 64$ | 0.67 | 11.04 | 63 | 0.76 | 0.06 | 45.02 | 76.31 | ||
| 2 | 2 | Proposed | $12\times 64$ | 0.33 | 9.90 | 24 | 0.66 | 0.05 | 1.20 | 12.46 |
| BAYES | $12\times 64$ | 0.67 | 11.04 | 63 | 0.78 | 0.45 | 3.20 | 16.31 | ||
| 3 | 4 | Proposed | $12\times 64$ | 0.33 | 9.90 | 24 | 0.30 | 0.00 | 1.83 | 18.04 |
| BAYES | $12\times 64$ | 0.67 | 11.04 | 63 | 0.66 | 0.16 | 240.96 | 535.21 | ||
| 4 | 4 | Proposed | $12\times 64$ | 0.33 | 9.90 | 24 | 0.65 | 0.06 | 1.48 | 12.77 |
| BAYES | $12\times 64$ | 0.67 | 11.04 | 63 | 0.63 | 0.46 | 4.61 | 30.40 | ||
| __________________ | _______________________ | __________________________ | __________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ | __________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ | __________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ | __________________________ | _____________________ | ___________________ | _____________________ | _____________________ |
| 5 | 4 | Proposed | $24\times 253$ | 0.33 | 21.84 | 168 | 0.60 | 0.00 | 1.61 | 21.59 |
| BAYES | $24\times 253$ | 0.67 | 22.91 | 252 | 0.67 | 0.00 | 3.62 | 27.99 | ||
| 6 | 4 | Proposed | $24\times 253$ | 0.33 | 21.84 | 168 | 0.70 | 0.05 | 1.85 | 29.70 |
| BAYES | $24\times 253$ | 0.67 | 22.91 | 252 | 0.61 | 0.28 | 3.36 | 50.61 | ||
| 7 | 6 | Proposed | $24\times 253$ | 0.33 | 21.84 | 168 | 0.54 | 0.00 | 4.24 | 38.37 |
| BAYES | $24\times 253$ | 0.67 | 22.91 | 252 | 0.67 | 0.28 | 162.70 | 934.85 | ||
| 8 | 6 | Proposed | $24\times 253$ | 0.33 | 21.84 | 168 | 0.72 | 0.01 | 3.49 | 25.34 |
| BAYES | $24\times 253$ | 0.67 | 22.91 | 252 | 0.70 | 0.44 | 16.57 | 158.04 |
Table 10
Comparison with the $UE({s^{2}})$-Optimal Designs.
| Case | #Active | Design | Size | μ | $E({s^{2}})$ | #Balance | MAFDR | MAMR | MMSE | MEME |
| 1 | 2 | Proposed | $12\times 64$ | 0.33 | 9.90 | 24 | 0.67 | 0.00 | 0.87 | 7.99 |
| JM | $12\times 64$ | 0.83 | 9.90 | 16 | 0.61 | 0.00 | 2.53 | 11.02 | ||
| 2 | 2 | Proposed | $12\times 64$ | 0.33 | 9.90 | 24 | 0.67 | 0.03 | 1.04 | 10.38 |
| JM | $12\times 64$ | 0.83 | 9.90 | 16 | 0.66 | 0.26 | 2.35 | 15.26 | ||
| 3 | 4 | Proposed | $12\times 64$ | 0.33 | 9.90 | 24 | 0.30 | 0.00 | 2.03 | 21.28 |
| JM | $12\times 64$ | 0.83 | 9.90 | 16 | 0.62 | 0.45 | 351.16 | 956.38 | ||
| 4 | 4 | Proposed | $12\times 64$ | 0.33 | 9.90 | 24 | 0.59 | 0.09 | 1.44 | 13.18 |
| JM | $12\times 64$ | 0.83 | 9.90 | 16 | 0.66 | 0.55 | 4.47 | 24.95 | ||
| __________________ | _______________________ | __________________________ | __________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ | __________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ | __________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ | __________________________ | _________________________ | _______________________ | ______________________ | ________________________ |
| 5 | 4 | Proposed | $24\times 256$ | 0.33 | 21.84 | 168 | 0.58 | 0.00 | 1.68 | 26.33 |
| JM | $24\times 256$ | 0.58 | 21.84 | 44 | 0.69 | 0.00 | 66.86 | 61.37 | ||
| 6 | 4 | Proposed | $24\times 256$ | 0.33 | 21.84 | 168 | 0.72 | 0.02 | 1.42 | 20.00 |
| JM | $24\times 256$ | 0.58 | 21.84 | 44 | 0.73 | 0.31 | 3.73 | 41.41 | ||
| 7 | 6 | Proposed | $24\times 256$ | 0.33 | 21.84 | 168 | 0.71 | 0.30 | 260.42 | 398.54 |
| JM | $24\times 256$ | 0.58 | 21.84 | 44 | 0.72 | 0.32 | 294.96 | 1336.26 | ||
| 8 | 6 | Proposed | $24\times 256$ | 0.33 | 21.84 | 168 | 0.62 | 0.35 | 13.62 | 110.92 |
| JM | $24\times 256$ | 0.58 | 21.84 | 44 | 0.72 | 0.43 | 18.54 | 147.44 |
3.4 Comparison with the $UE({s^{2}})$-Optimal Designs
According to Jones and Majumdar [15], for given n and p, there are a large number of $UE({s^{2}})$-optimal designs. In practical scenarios, people may randomly generate only one $UE({s^{2}})$-optimal design and use it to screen important factors. In our comparison, we want to mimic such a scenario, i.e., we want to know whether people will have a higher chance ($\gt 0.5$) of getting a worse design (compared with our design) if they generate a $UE({s^{2}})$-optimal design in this way. Therefore, we randomly generate 500 $UE({s^{2}})$-optimal designs and for each of them, repeat the simulation procedure $N=30$ times (rather than $N=300$ in comparisons with other competing designs). We take the median values for the four criteria introduced in the beginning of the section over the 500 randomly generated designs and compare these median values with the corresponding criteria of the proposed design. If the AFDR of a proposed design is less than the median AFDR (MAFDR) of all the 500 $UE({s^{2}})$-optimal designs, it means the AFDR of the proposed design is less than that of the $UE({s^{2}})$-optimal design with more than half probability. The coherence, $E({s^{2}})$ and number of balanced columns in the table are also the corresponding medians. In addition, it is possible that a generated $UE({s^{2}})$-optimal design has $\mu =1$ and we will avoid using these designs in the simulations, because in practice if people get a bad design with $\mu =1$, they will probably regenerate another one.
We use the $12\times 64$ and $24\times 256$ proposed designs in Example 1 directly. We obtain the $UE({s^{2}})$-optimal designs by randomly sampling 12 rows of a $64\times 64$ Hadamard matrix 500 times and 24 rows of a $256\times 256$ Hadamard matrix 500 times, respectively. The result shown in Table 10 indicates that with more than half probability, the proposed designs outperform the $UE({s^{2}})$-optimal designs in terms of variable selection and parameter estimation with the Lasso. Furthermore, one may want to see the distributions of the criteria of 500 $UE({s^{2}})$-optimal designs. We take Case 8 for an example and show the distributions of the criteria in Figure 1.
Figure 1
Comparison between the $UE({s^{2}})$-optimal design and the proposed design in Case 8. The solid curves are the kernel density estimates of the probability density functions of $UE({s^{2}})$-optimal design’s criteria and the solid lines are the corresponding median values. The dashed lines are the values of the proposed design’s criteria.
3.5 Summary of Comparisons
To help people better understand how the proposed design performs compared to competing designs with the same size and under the same active coefficient setting, we collect the comparisons between designs with exactly the same size and active coefficient setting all together in Table 11. Lin’s design is not of size $12\times 64$, so it is not included in the table (it is actually impossible to construct a design of this size with Lin’s method).
Table 11
Comparison Between Designs with the Same Size and Active Coefficients.
| Case | #Active | Design | Size | μ | $E({s^{2}})$ | #Balance | AFDR | AMR | MSE | EME |
| 1 | 2 | Proposed | $12\times 64$ | 0.33 | 9.90 | 24 | 0.65 | 0.00 | 0.95 | 8.41 |
| WU | $12\times 64$ | 0.33 | 11.06 | 63 | 0.54 | 0.00 | 0.89 | 9.03 | ||
| BAYES | $12\times 64$ | 0.67 | 11.04 | 63 | 0.76 | 0.06 | 45.02 | 76.31 | ||
| JM | $12\times 64$ | 0.83 | 9.90 | 16 | 0.61 | 0.00 | 2.53 | 11.02 | ||
| 2 | 2 | Proposed | $12\times 64$ | 0.33 | 9.90 | 24 | 0.66 | 0.05 | 1.20 | 12.46 |
| WU | $12\times 64$ | 0.33 | 11.06 | 63 | 0.56 | 0.04 | 0.98 | 11.22 | ||
| BAYES | $12\times 64$ | 0.67 | 11.04 | 63 | 0.78 | 0.45 | 3.20 | 16.31 | ||
| JM | $12\times 64$ | 0.83 | 9.90 | 16 | 0.66 | 0.26 | 2.35 | 15.26 |
According to Table 11, the proposed design significantly outperforms the Bayesian D-optimal design and the $UE({s^{2}})$-optimal design. In this scenario, Wu’s design performs slightly better than the proposed design, but there are also scenarios where the proposed design performs better than Wu’s design (see Table 8).
In summary, for Wu’s design, the proposed design is generally comparable to it, because of the same coherence they have. For Lin’s design, the Bayesian D-optimal design and the $UE({s^{2}})$-optimal design, the proposed design generally outperforms them, except that it sometimes tends to select more factors and gives a larger AFDR. However, the proposed design always gives a smaller AMR when compared to these three designs. In practice, a small AMR is more important than a small AFDR, because missing active factors is a more serious problem than falsely discovering inactive factors. This is because we can conduct follow-up experiments to screen out spurious factors, but we can never detect active factors that were already removed in the screening phase [21].
4 Conclusion and Discussion
We have proposed a method for constructing supersaturated designs with small coherence. The constructed designs are allowed to be unbalanced to achieve more flexible sample sizes. The proposed method uses direct constructions and it entails no intensive computing even for large p. Since the proposed method can efficiently construct a supersaturated design with a large number of columns, it can be applied to high-dimensional variable selection problems in marketing, biology, engineering and other areas.
Here are possible directions for future work. First, the proposed method can expand a $6m\times p$ design ${\mathbf{D}_{0}}$ with $\mu \le 1/3$ to a larger design with $\mu \le 1/3$. One may be interested in finding a special ${\mathbf{D}_{0}}$ such that the expanded design has coherence strictly smaller than $1/3$ or using a different construction method to reduce the coherence upper bound. Second, beyond the Lasso, the proposed design can be applicable to other variable selection and high-dimensional problems where controlling coherence of the design matrix is important. Moreover, many new powerful variable selection techniques have emerged. For example, Fan and Lv [10] and Fan, Feng and Song [11] proposed the sure independence screening and nonparametric independence screening for ultrahigh dimensional variable selection. Another example is the best subset regression. Shen, Pan, Zhu and Zhou [25] provided theoretical support for the use of best subset regression. Bertsimas, King and Mazumder [1] proposed a mixed integer optimization approach for the best subset selection problem, where they showed that coherence plays a role in parameter specification of their approach. In future work, our proposed designs will be applied to other penalized variable selection methods with results reported elsewhere.

